Content tagged self-driving-car

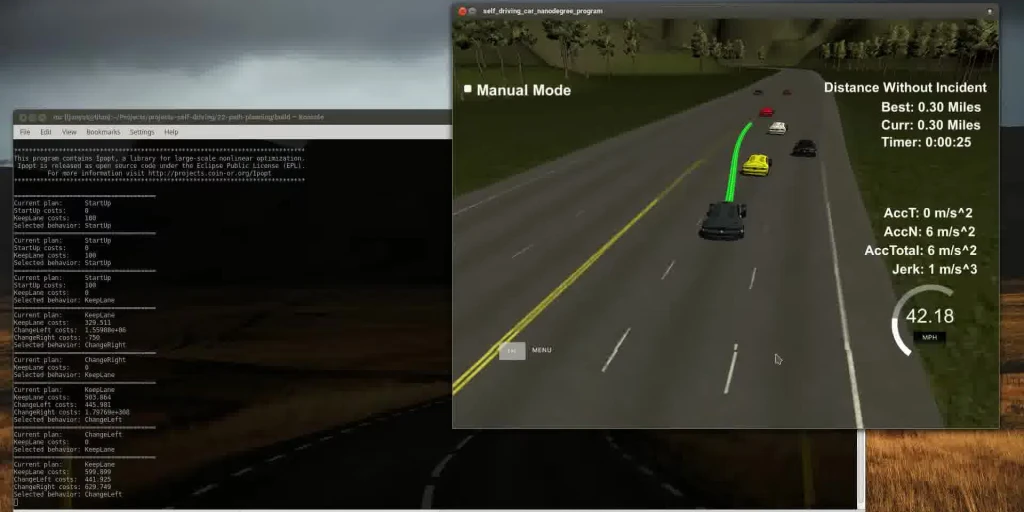
This post describes another one of the Udacity Self-driving Car Nanodegree projects. The goal is to plan a path or a car through highway traffic. You have to obey the rules, pay attention not to collide with anyone, and minimize jerk. I used a non-linear optimizer (Ipopt) and massaged the code I wrote for model-predictive control. Things worked out quite nicely.

Semantic segmentation is a process of dividing an image into sets of pixels sharing similar properties and assigning one of the pre-defined labels to each of these sets. Or, in other words, you get a picture, and you're supposed to tell which pixels constitute a car and which constitute the pedestrians. Fun stuff.

Playing with particle filters. They are a cool way to estimate a robot's position based on noisy signals and using randomness.

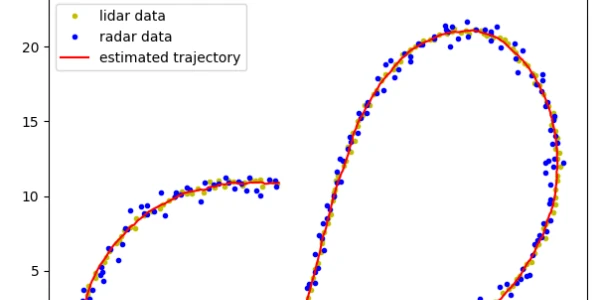
Estimating a trajectory of an object using Kalman filters based on radar and lidar data.

In this post, I am playing with some classical computer vision algorithms and Support Vector Machines to see where the lane lines and other vehicles are in a video taken by a front-facing camera in a car driving on a highway.

You get to drive a car in a game capturing some images and the corresponding steering angle. You then use that data to build a neural network that spits out a steering angle for an input image such that the computer can drive the same car in the same game. The computer learns how to drive from you, hence behavioral cloning.