Content tagged math

There was no understandable and straightforward implementation of SSD in TensorFlow, so I decided to make one. The original paper assumes familiarity with related research, so I needed to plow through several additional papers and a ton of source code to understand what's going on here. This post is an attempt to provide all that missing context in one place.

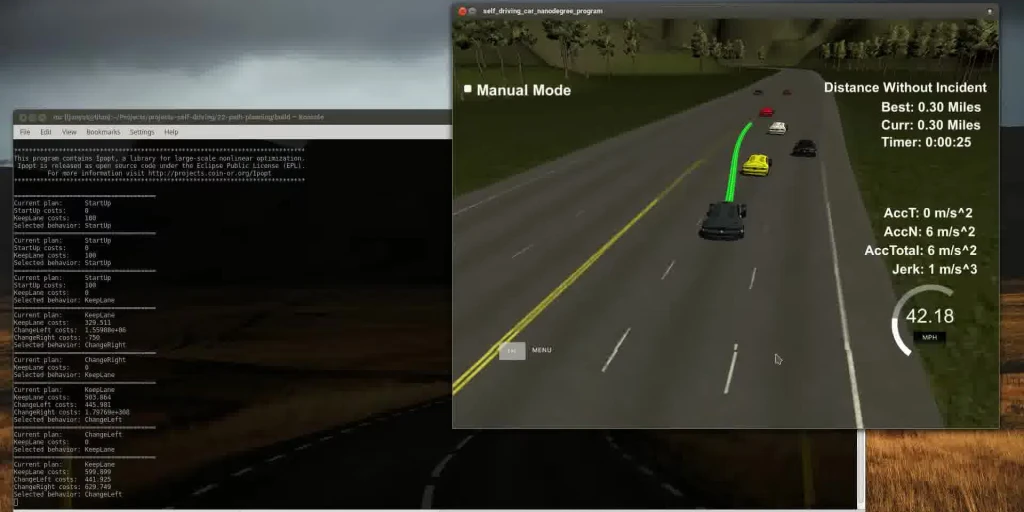
This post describes another one of the Udacity Self-driving Car Nanodegree projects. The goal is to plan a path or a car through highway traffic. You have to obey the rules, pay attention not to collide with anyone, and minimize jerk. I used a non-linear optimizer (Ipopt) and massaged the code I wrote for model-predictive control. Things worked out quite nicely.

Fun with shuffling file contents using a splay tree.